Investigating the spatial and environmental factors explaining the distribution of motor vehicle crashes in Austin, Texas.
Traffic crashes are a major safety and infrastructure concern for cities. While some crash locations may be explained by obvious factors like traffic volume or road geometry, others may be influenced by less visible spatial drivers such as speed limits, construction zones, or socioeconomic conditions.
This project used spatial regression techniques — including Ordinary Least Squares (OLS) and Geographically Weighted Regression (GWR) — to explore potential spatial predictors of crash incidence across Austin. These methods helped assess both global relationships and local variation in model performance.
Study area
The study focused on the city of Austin, Texas.
According to the U.S. Census Bureau, Austin was the 13th most populous city in 2024. As its population continues to grow, Austin faces increasing pressure on its road infrastructure, posing challenges for traffic safety, urban planning, and policy response.
Data
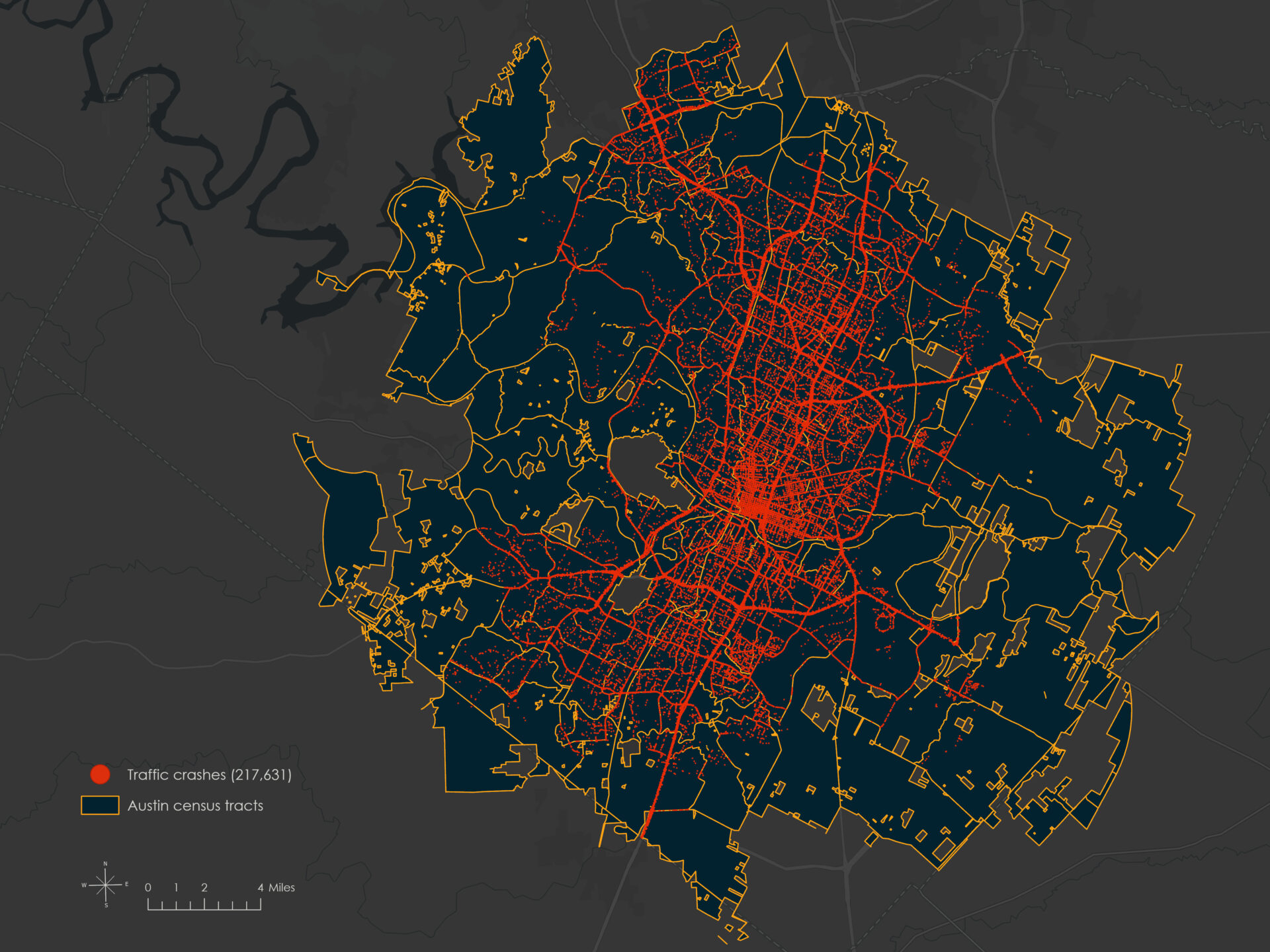
For this project, traffic crash data were obtained from the City of Austin’s open data portal, which includes detailed point-based records of reported traffic crashes. The study area also incorporates base layers such as road classifications from TIGER/Line and demographic context from the U.S. Census Bureau.
| Layer | Source | Dataset / service | Variables |
|---|---|---|---|
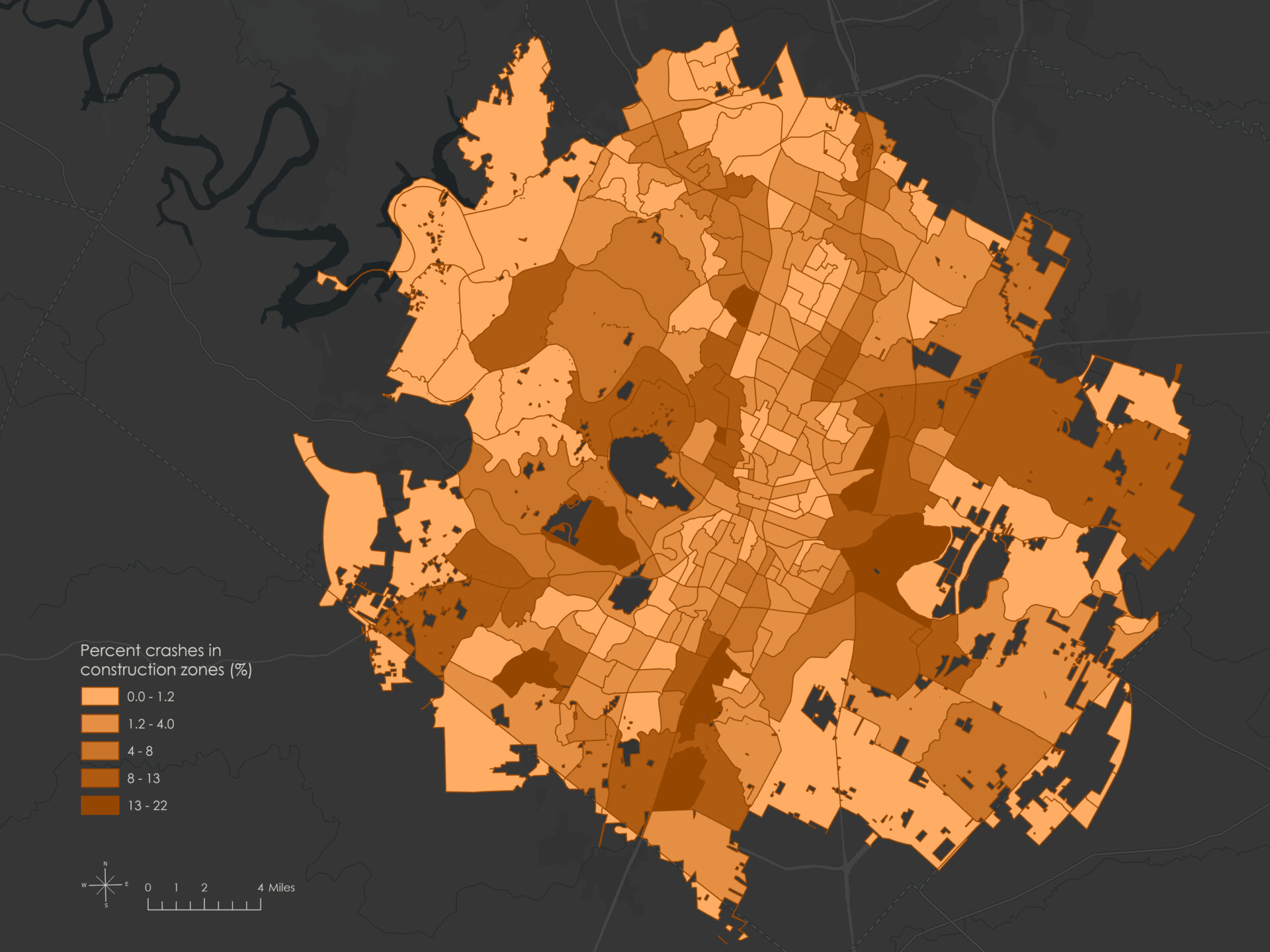
| Crash incidents | City of Austin Open Data Portal | Austin Crash Report Data – Crash Level Records | Crash countAvg speed limitPercent construction zone |
| Roads | U.S. Census Bureau | TIGER/Line Shapefiles (Travis county) | Percent primary roads |
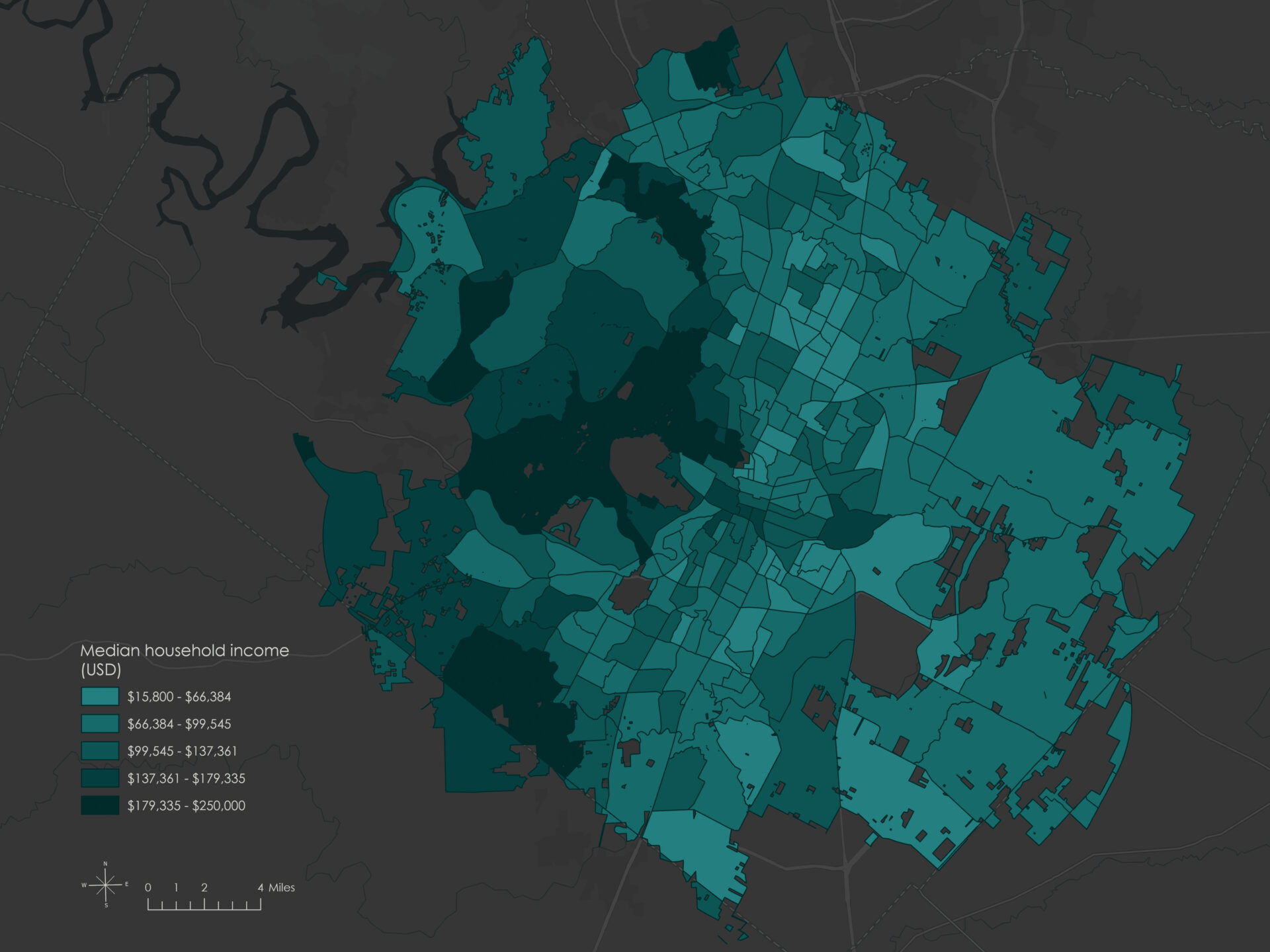
| Median household income | Esri | ACS Median Household Income Variables – Boundaries | Median income |
| Census tracts | Esri | USA Census Tract Boundaries | Population density |
| Austin | City of Austin Open Data Portal | BOUNDARIES_jurisdictions |
All spatial data were downloaded on August 7, 2025, clipped to Austin city limits, and projected to NAD 1983 StatePlane Texas Central FIPS 4203 (Feet), which provided high spatial accuracy for this city-scale analysis.
All analyses were conducted at the census tract level to ensure consistency in spatial scale and data availability. Only tracts within the Austin city limits were included, based on a jurisdictional boundary clip.
Dependent and explanatory variables
Dependent variable: Crash count per census tract (January 2010 – July 2025)
Explanatory variables:
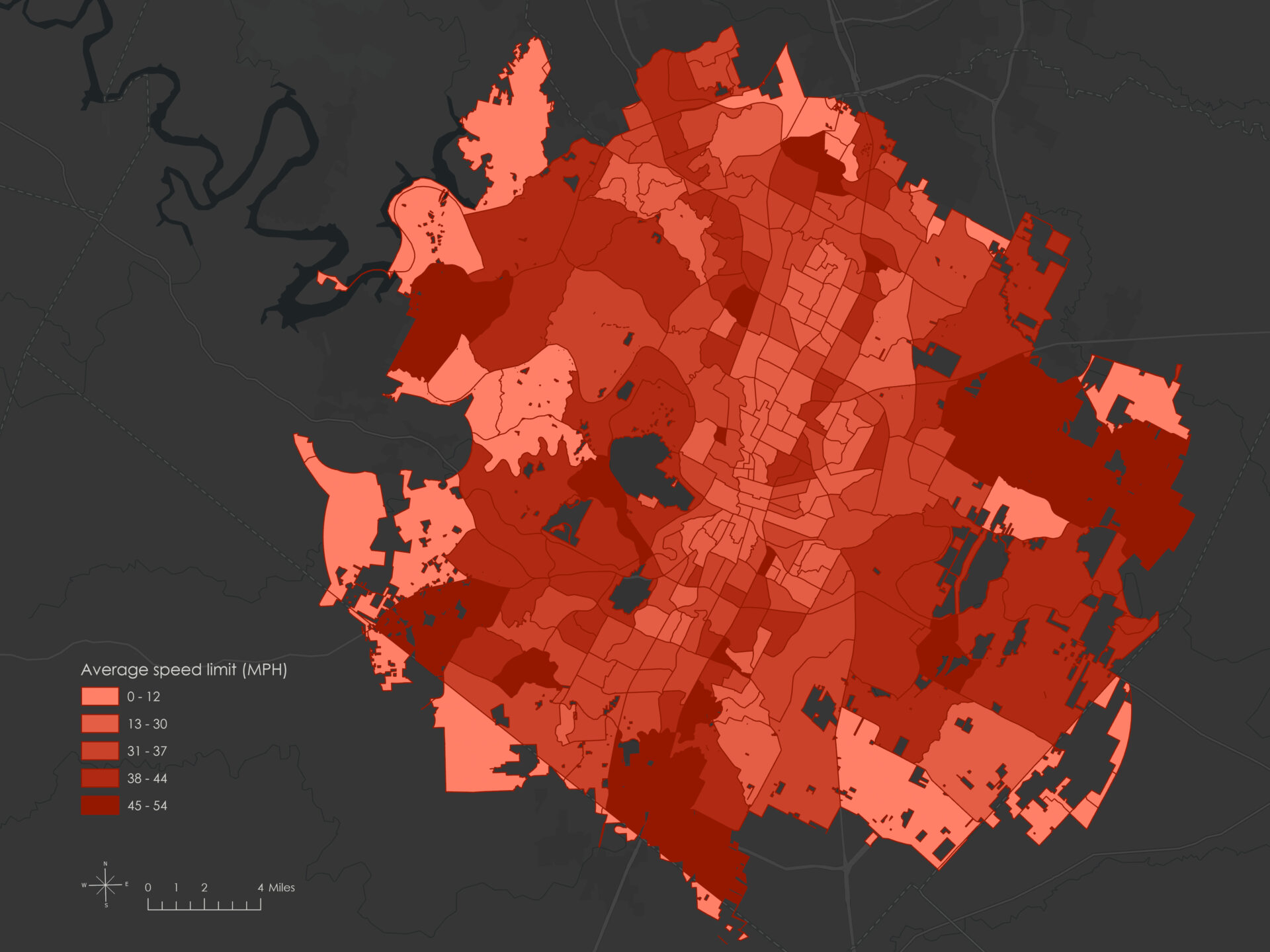
- Average speed limit (MPH) — Represents the average traffic speed limit in each census tract, calculated as the mean posted speed limit of all crash locations in that tract.
- Percent primary roads — The proportion of total road mileage in each census tract classified as Interstate (I), U.S. Route (U), or State Route (S) according to U.S. Census Bureau TIGER/Line RTTYP codes.
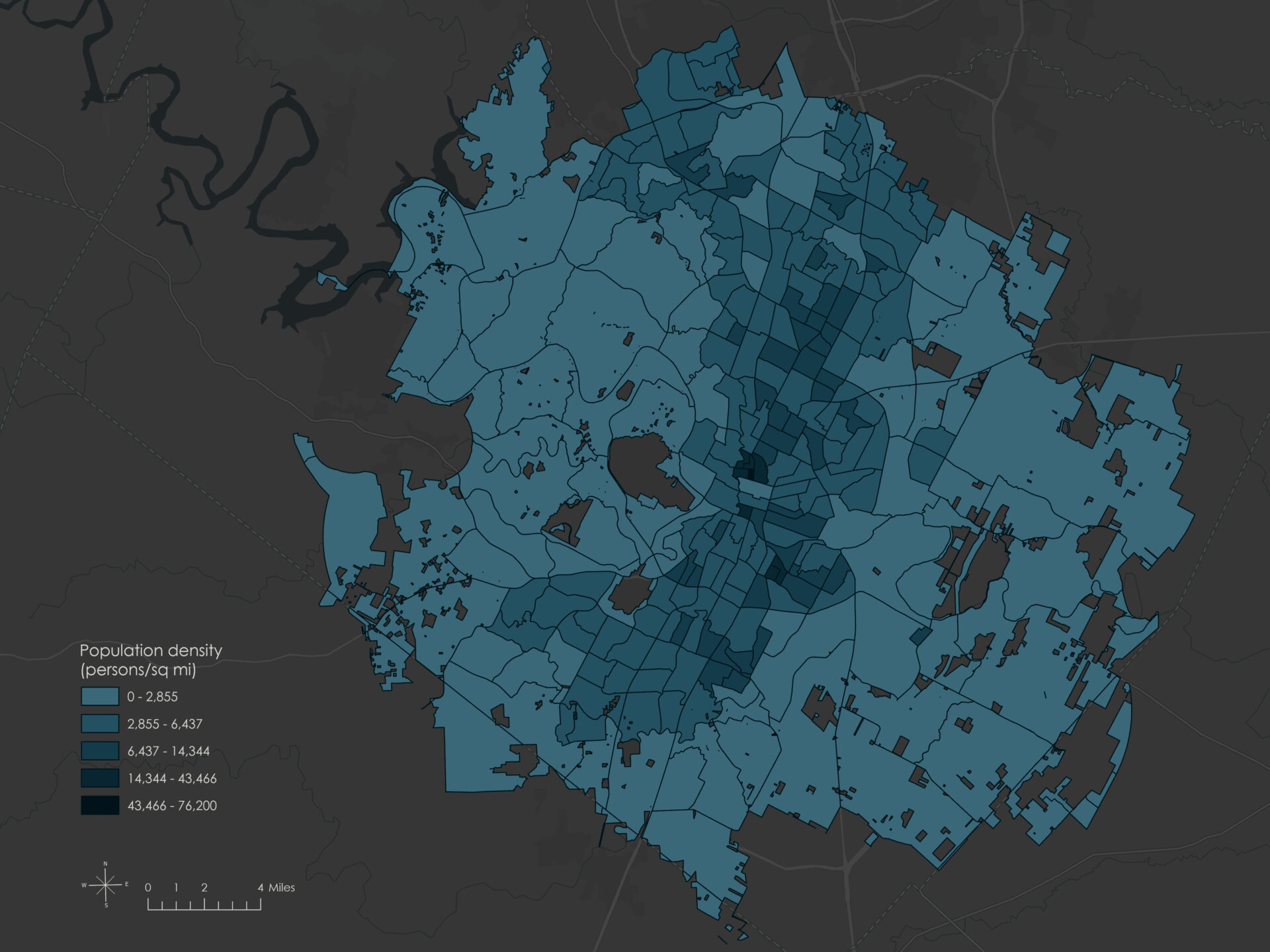
- Population density (persons per square mile) — Measures potential exposure to traffic incidents by normalizing population counts to land area.
- Percent of crashes in construction zones — Indicates whether crashes occurred in a construction, maintenance, or utility work zone (regardless of whether or not workers were actually present at the time of the crash), calculated as the proportion of all crashes.
- Median household income (USD) — Socioeconomic factor from ACS 5-Year Estimates, representing the median annual income of households in each census tract.

For explanatory regression, the minimum Adjusted R² threshold was set at 0.5 to prioritize models with stronger fit, and the maximum acceptable Variance Inflation Factor (VIF) was set at 7.5 to avoid multicollinearity.
For Moran’s I and GWR, Euclidean distance and inverse distance weighting were used to conceptualize spatial relationships.
Null values in explanatory fields were treated as zeros where conceptually appropriate (e.g., road mileage, crash counts), based on the assumption that no data implies absence of feature.
Exploratory regression analysis
Exploratory Regression is used to identify combinations of explanatory variables that best explain variation in a dependent variable. The tool tests all variable combinations within defined limits and evaluates each resulting model using criteria like adjusted R², multicollinearity (VIF), residual normality (Jarque–Bera), nonstationarity (Koenker), and spatial autocorrelation. The process helps identify promising models and flag issues.
The three highest-performing models included combinations of Avg speed limit, Median income, Percent construction zone, Percent primary roads, and Population density.
The top model included the Avg speed limit, Median Household Income, and Percent construction zone variables.
| AdjR2 | AICc | JB | K(BP) | VIF | SA | Model |
|---|---|---|---|---|---|---|
| 0.25 | 4643.37 | 0.00 | 0.01 | 1.40 | 0.00 | +Avg speed limit*** –Median income*** +Percent construction zone* |
It had an adjusted R² of 0.25, indicating 25% of the variation in Crash count was explained. AICc was 4643, the lowest among all models tested. VIF was low (1.40), suggesting no multicollinearity.
However, the model failed both the Jarque–Bera (0.00) and Moran’s I (0.00) tests, indicating residuals were non-normal and spatially autocorrelated.
The Koenker p-value (0.01) suggests nonstationarity, warranting follow-up with Geographically Weighted Regression (GWR) analysis.
Ordinary Least Squares (OLS) analysis
Before moving on to the GWR analysis, I ran the top model through Ordinary Least Squares (OLS), a global regression method that quantifies the relationship between one dependent and multiple explanatory variables. OLS serves as a baseline model before testing more spatially flexible approaches.
| Variable | Coefficienta | StdError | t-Statistic | Probabilityb | Robust_SE | Robust_t | Robust_Prb | VIFc |
|---|---|---|---|---|---|---|---|---|
| Intercept | 445.009522 | 127.158847 | 3.499635 | 0.000551* | 87.330086 | 5.095718 | 0.000001* | ——– |
| Avg speed limit | 18.673691 | 3.110208 | 6.004002 | 0.000000* | 2.599931 | 7.182380 | 0.000000* | 1.403958 |
| Median income | -0.003159 | 0.000799 | -3.956042 | 0.000103* | 0.000631 | -5.006675 | 0.000002* | 1.022640 |
| Percent construction zone | 20.553942 | 10.261864 | 2.002944 | 0.046104* | 11.204707 | 1.834402 | 0.067618 | 1.395238 |
The OLS results confirmed both the statistical significance and expected direction of the explanatory variables. Avg speed limit had a strong positive effect on Crash count, while Median income had a negative association, and Percent construction zone showed a weaker but still notable positive relationship.
The adjusted R² remained at 0.25, and variance inflation factors (VIF) were low, suggesting no multicollinearity.
The histogram and scatterplots below show the distributions and relationships between the explanatory variables and the dependent variable (Crash count). Residual plots suggest non-normality and variance inconsistencies.
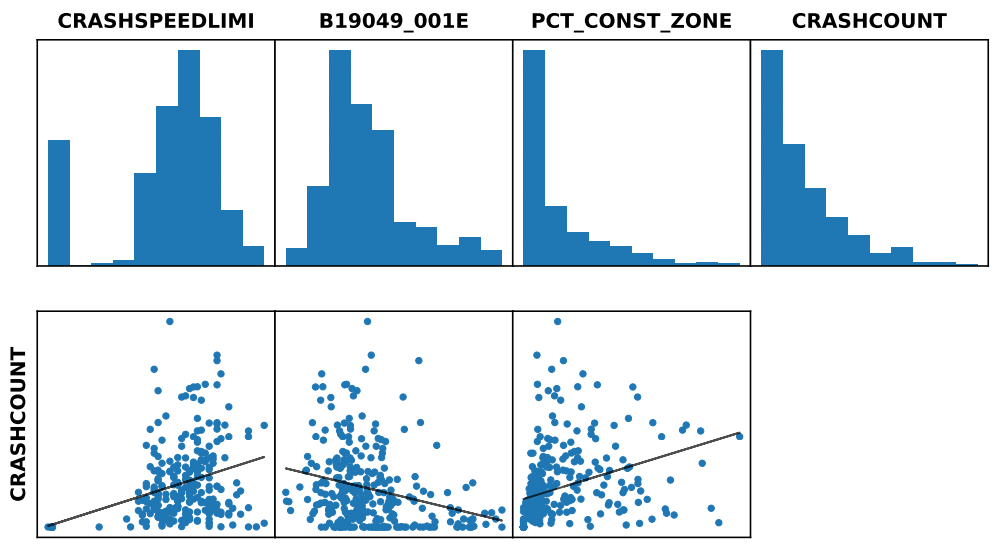
Again, the model failed the Jarque-Bera, Koenker, and Moran’s I tests, reinforcing the need to proceed with a geographically weighted regression to better capture local variation in explanatory variable effects.
The standardized residual histogram below further illustrates deviation from normality, with a skewed distribution and multiple outliers.
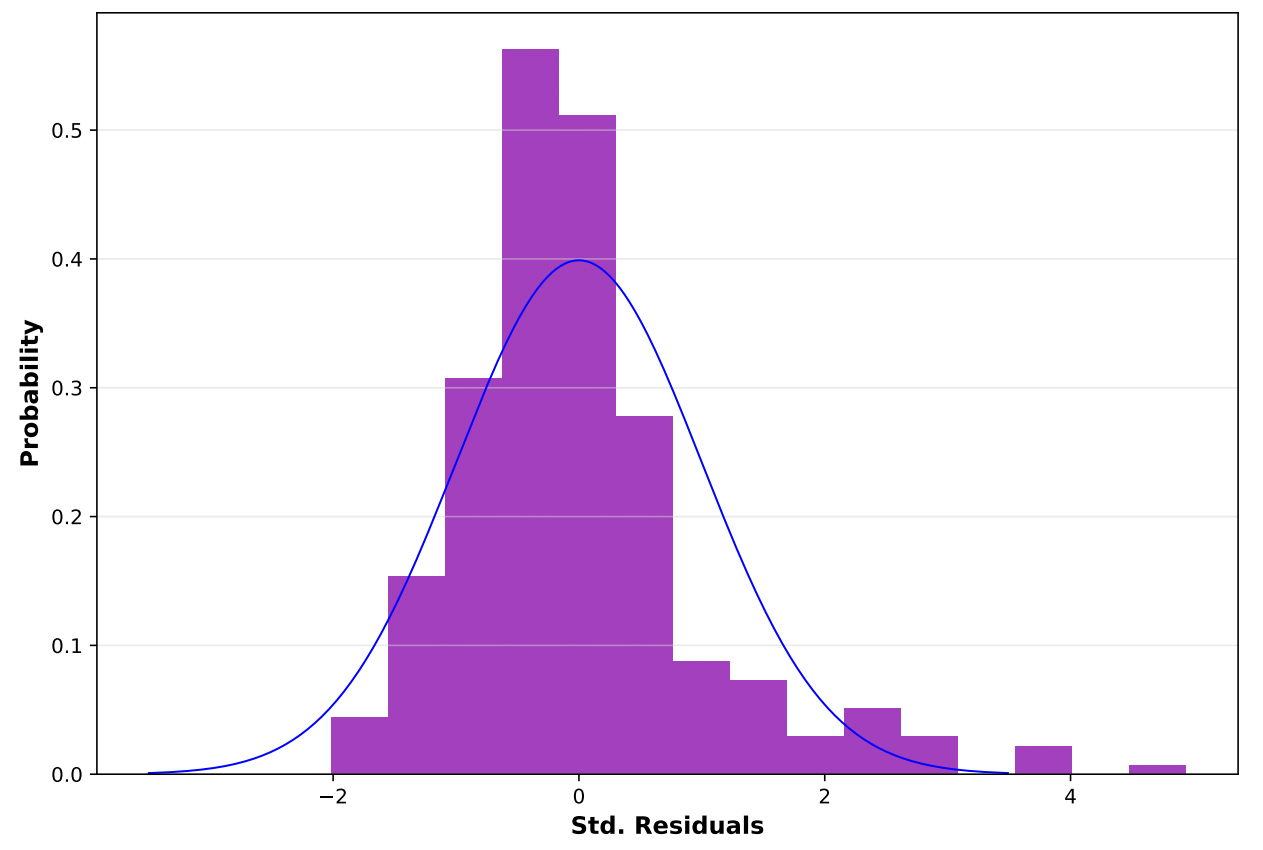
The Joint Wald statistic was significant (p < 0.01), confirming the overall explanatory power of the model despite heteroskedasticity or nonstationarity.
To evaluate spatial dependence in model errors, residuals from the OLS model were tested using the Spatial Autocorrelation (Global Moran’s I) tool. A Moran’s I value of 0.149, a z-score of 7.59, and a p-value < 0.0001 indicate strong and statistically significant spatial autocorrelation in the residuals.
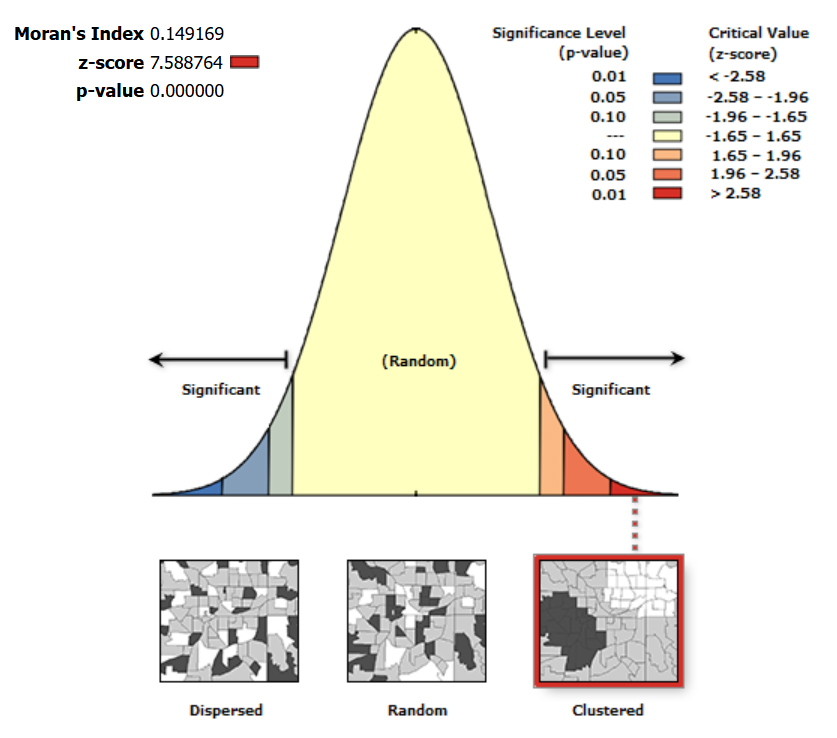
This shows that the OLS model’s residuals are clustered, violating one of the key assumptions of OLS and reinforcing the need to use Geographically Weighted Regression to better capture local spatial variation in crash patterns.
Geographically weighed regression (GWR) analysis
Geographically Weighted Regression (GWR) is a local form of linear regression that models spatially varying relationships throughout a study area. Unlike global models like Ordinary Least Squares, which assume that the relationship between variables is constant across space, GWR applies a regression equation at each location in the dataset. This allows it to account for spatial variation (nonstationarity).
The relationship between my dependent variable (Crash count) and my explanatory variables was nonstationary. The OLS model failed the Koenker and Moran’s I tests, indicating inconsistent relationships and spatial clustering in the residuals.
| Number of Features | 295 |
| Dependent Variable | Crash count |
| Explanatory Variables | Avg speed limit |
| Median income | |
| Percent construction zone | |
| Number of Neighbors | 69 |
The GWR model used 69 neighbors and produced an R² of 0.55 and an adjusted R² of 0.44. Sigma-squared was 291,584, and the model used an effective 236 degrees of freedom.
These statistics indicate a better model fit compared to OLS. The improvement in R² and drop in AICc validated the need for a geographically weighted approach.
GWR vs OLS model comparison
| Metric | GWR | OLS |
|---|---|---|
| R² | 0.5527 | 0.2563 |
| Adjusted R² | 0.4400 | 0.2486 |
| AICc | 4,592.97 | 4,643.37 |
| Effective Effective Degrees of Freedom | 235.82 | n/a |
| Sigma-Squared | 291,584 | n/a |
These results confirm that the influence of explanatory variables such as Avg speed limit and Percent construction zone varies across the city and cannot be adequately explained by a global regression model.
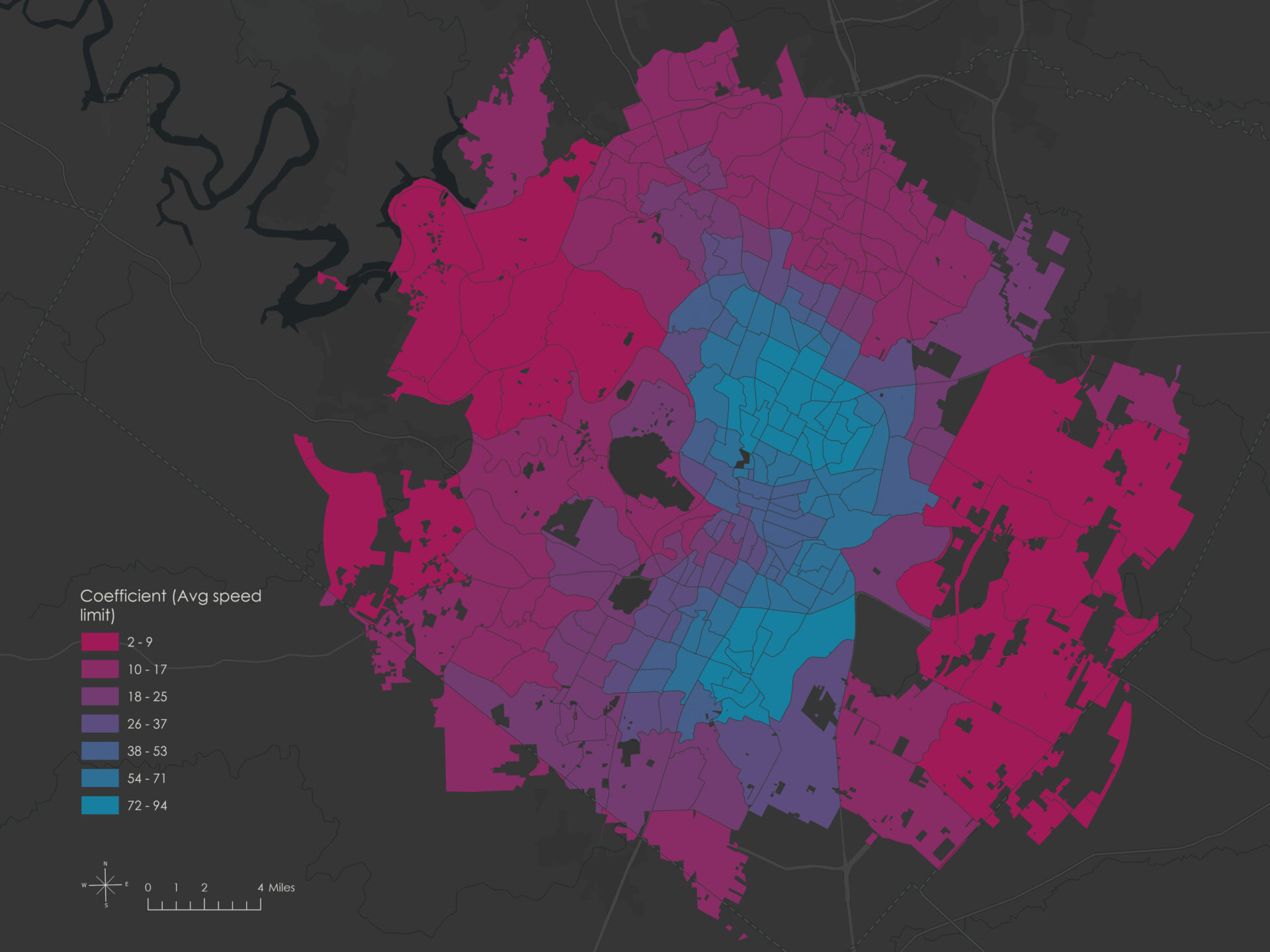
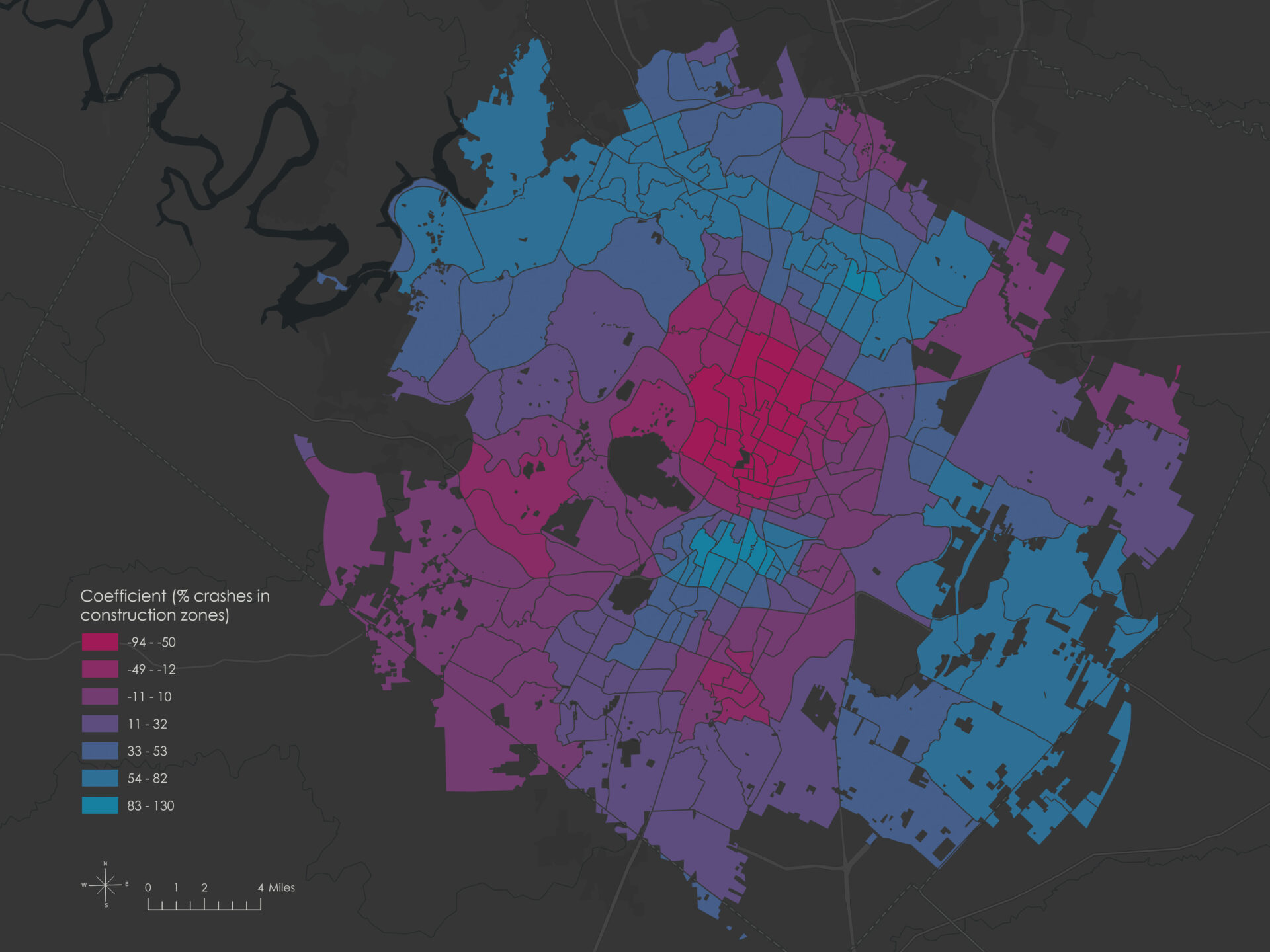
These maps show the local Avg speed limit and Percent construction zone coefficients from the GWR model.
- Large positive values indicate a strong positive influence (crash counts increase as the variable increases).
- Large negative values indicate strong negative influence (crash counts decrease as the variable increases).
- Values near zero suggest weak or no relationship in that location.
Conclusions
The spatial regression analysis identified Avg speed limit, Median income, and Percent construction zone as the most consistent predictors of Crash count at the census tract level in Austin.
The global OLS model explained 25% of the variation in crash counts, while the GWR model was able to explain 55% of the variation due to its strength in accounting for spatial nonstationarity.
Overall, though, the models did not identify strong, consistent predictors of Crash count. Avg speed limit had a positive association, but the effects of Percent construction zone and Median income were weaker and varied widely across space. I believe that the results of the regression models indicate key explanatory variables are likely still missing.
Several limitations affect the strength and interpretation of these results. First, Crash count is an imperfect dependent variable (it is influenced by population, traffic volume, and reporting practices).
Second, the explanatory variables were approximated and sometimes dated. For example, construction zone presence was treated as a binary attribute, speed limit was averaged per tract, and census data may not reflect current socioeconomic conditions.
Finally, the analysis was constrained by data availability and quality, including handling of NULL values in the potential explanatory variable datasets.
Citations
City of Austin Transportation Public Works. Vision Zero Viewer. https://visionzero.austin.gov/viewer/.
City of Austin Open Data Portal. Austin Crash Report Data – Crash Level Records [Data set]. https://data.austintexas.gov/Transportation-and-Mobility/Austin-Crash-Report-Data-Crash-Level-Records/y2wy-tgr5/about_data.
City of Austin Open Data Portal. BOUNDARIES_jurisdictions [Data set]. https://data.austintexas.gov/dataset/BOUNDARIES_jurisdictions/3pzb-6mbr.
Esri. ACS Median Household Income Variables – Boundaries [Data set]. ArcGIS Online. https://www.arcgis.com/home/item.html?id=45ede6d6ff7e4cbbbffa60d34227e462.
Esri. USA Census Tract Boundaries [Data set]. ArcGIS Online. https://www.arcgis.com/home/item.html?id=20f5d275113e4066bf311236d9dcc3d4.
U.S. Census Bureau. Population Growth Reported Across Cities and Towns in All U.S. Regions. https://www.census.gov/newsroom/press-releases/2025/vintage-2024-popest.html.
U.S. Census Bureau. 2024 TIGER/Line Shapefiles: Roads [Data set]. https://www.census.gov/cgi-bin/geo/shapefiles/index.php?year=2024&layergroup=Roads.